Servo Torque and Speed Calculator
Sheet travel for any boom angle when C = B
User Guide
This Calculator will allow you to try different combinations of measurements to maximise the characteristics of your boat and available servos. For example, you will quickly see the effect of moving the sheet (cord) attachment point on the Boom.
Wind Speed
Unless you have an anemometer to measure the wind speed at your sail height. Your only other way to estimate wind speed is to use the Beaufort Scale.
This brings introduces its own problem as Beaufort wind speed is given at 10m. Wind Gradient is the rate at which the wind speed reduces as it approaches zero at ground level. This calculator computes the wind force at the sail‘s centre of effort using a wind gradient formula.
Sail Forces
The calculator uses “Turning Moments” to compute the load on the sheet as it passes through the deck from the force on the sail.
Sail Factors.
To calculate some of these dimensions, you might find it easier to cut a paper template of your sail
1) Sail Area sq cm. Determines how much of the wind‘s energy is converted into the boat‘s speed.
The area of a triangular sail is its base times half height. For complex shapes draw parallel lines 2 or 3cm apart from the longest straight side on the paper template. Make each set of lines into rectangles leaving a triangle at the end. Calculate the area of each part. Cut and paste into a rectangle.
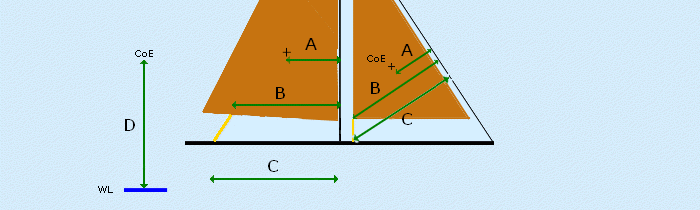
2) Centre of Effort. This is the point at which the wind force acts on the sail.
To find the CofE, hold the sail paper template vertically by one corner with a pin, draw a vertical line down from the pin and repeat for all corners. CofE is the middle of the crossed lines.
3) CofE to Point of Rotation cm. (a) the distance between the CofE and the Mast edge or sail luff. (at 90 deg.)
4) CofE to Sheeting Point cm. (b) the distance between the sail cord attachment point and mast edge or sail luff. (at 90 deg).
5) Deck Sheeting Point to Point of Rotation cm. (c) the distance between the point the cord passing through the deck to mast edge or sail luff. (at 90 deg).
Variables
6) Sail Foot. When a sail is attached to a boom the sail sheet is at an angle to the boom and wind direction. The force on the sail sheet has to be increased to compensate for the commpression force on the boom. 90 degrees is used as a standard.
Without the boom, the sheet load is calculated with the sail sheet inline with the wind direction.
7) Factor of Safety. It is common practice in engineering to use a Factor of Safety of 2 which will double the sheet load. Equivalent to a gust of wind increasing the wind factor by one. It will take friction into account and the boom slamming over.
8) Safe Working Load. Electric motors do not produce usable power if their speed drops off. Three levels are available which are used to calculate a servo‘s required Stall Torque as this is the only data given by the manufacturers.
Lower the value, the higher the stall torque required.
Analog servo‘s sheet travel reduces as the power/speed reduces.
Sheet Speed
Drum diameter/circumference, sheet travel and time are used to calculate the servo‘s rotational speed.
9) Sheet Travel cm. Measure the boat’s actual sheet travel. If unknown, the calculator will work this out for you with the boom at 90 degrees.
The second calculator will work this out for you if you know the distance B between the sheet attachment point to pivot point and the boom angle.
10) Sheet Times sec. Time to pull in your sail sheet.
11) Drum Diameter cm. Leave blank if you don’t know this value, the calculator will show values at 2.5, 3 and 4cm. Increasing drum diameter reduces speed.
Typical measurements
| Measurements | One Meter | Marblehead | Jolie Brise | |||
|---|---|---|---|---|---|---|
| Main | Fore | Main | Fore | 1/20 Main+Top | 1/10 Main+Top |
|
| Sail Area cm2 (dm2) | 3468 (35dm2) | 2458 (25dm2) | 2990 (30dm2) | 2140 (21dm2) | 3310 (33dm2) | 13240 (132dm2) |
| (a) CoE to PoR | 12 | 6.2 | 13 | 13 | 21 | 48.3 |
| (b) Sheet to PoR | 32 | 19 | 28 | 41 | 21 | 50 |
| (c) Deck to PoR | 32 | 19 | 28 | 41 | 21 | 50 |
| (d) CoE to WL | 61 | 48 | 103 | 62 | 51 | 103 |
| Windspeed | 4 | 4 | 4 | 4 | 4 | 4 |
| Safety Factor | 2 | 2 | 2 | 2 | 2 | 2 |
| SWL % | 20 | 20 | 20 | 20 | 20 | 20 |
| Sheet Travel | 45 | 67 | 40 | 58 | 30 | 60 |
| Sheet Time | 5 | 5 | 5 | 5 | 6 | 7 |
| Drum Diameter | 4 | 4 | 4 | 4 | 4 | 4 |
The figures for One Metre and Marblehead have been scaled from drawings. Please contact me with actual dimensions
The calculator uses Force x Distance = Torque. Distances are from the Point of Rotation PoR to the Point of the Load. Triangulation of forces are used to calculate the sheet force with the Boom out at 90°.
The height of the Centre of Effort CoE above the waterline is important as it works out the Wind Force for the height of your boat and not at the standard height of 10m. It’s a complex formula easily computed.
Results for One Meter, Marblehead and Jolie Brise
| Results | One Meter | Marblehead | Jolie Brise | |||
|---|---|---|---|---|---|---|
| 4cm Drum | Main | Fore | Main | Fore | 1/20 Main+T | 1/10 Main+T |
| Sheet Load Kg | 0.26 | 0.14 | 0.36 | 0.14 | 0.66 | 3.26 |
| Torque Kg.cm | 0.51 | 0.28 | 0.71 | 0.27 | 1.32 | 6.52 |
| Stall Torque | 2.6 | 1.4 | 3.6 | 1.4 | 6.6 | 32.6 |
| Speed sec/100mm | 1.1 | 0.7 | 1.3 | 0.9 | 2.0 | 1.2 |
| Drum Turns | 3.6 | 5.3 | 3.2 | 4.6 | 2.4 | 4.8 |
| Time for 1 Turn | 1.4 | 0.9 | 1.6 | 1.1 | 2.5 | 1.5 |
| Time for 60 deg | 0.2 | 0.2 | 0.3 | 0.2 | 0.4 | 0.2 |